I’m currently re-reading Michael Mauboussin’s Success Equation. The book is a discussion about the roll both skill and luck play in business and sport success. On page 118, Mauboussin discusses the Mathew Effect. The Mathew Effect, termed by sociologist Robert Merton, comes from a phrase in the bible written in the Gospel of Matthew:
“For whosoever hath, to him shall be given, and he shall have more abundance: but whosoever hath not, from him shall be taken away even that he hath.”
In a nutshell, the Mathew Effect is describing the phenomenon, “the rich get richer and the poor get poorer”.
Mauboussin goes on to provide an example of two graduate students, both with equal ability. Following graduation, the two students are applying for faculty positions. One is hired by an Ivey League university while the other goes to work at a less prestigious university. The Ivey League professor has a wonderful opportunity with perhaps more qualified students, high caliber faculty peers, and more funding for research. Such an opportunity leads to more scientific publications and greater notoriety and accolades in comparison to their peer at the less prestigious university.
As Mauboussin says, “initial conditions matter”. Both students had the same level of skill but different levels of luck. Student one’s initial condition of obtaining a faculty position at an Ivey League university set her up for better opportunities in her professional career, despite not being any more talented than student two.
Such an example applies in many areas of our lives, not just sport and business. For example, in the educational sector, some students may grow up in areas of the country where the public school environment does not provide the same educational experience that more affluent regions might. These students may not be any less intelligent than their peers, however, their initial conditions are not the same, ultimately having an influence in how the rest of their life opportunities turn out and how things look at the finish line.
Luck ends up playing a big role in our lives and the starting line isn’t the same for everyone. Mauboussin refers to this as preferential attachment, whereby the more connections you start with in life, the more new connections you are able to make. To show this concept, Mauboussin creates a simple game of drawing marbles from a jar (pg. 119):
We have a jar filled with the following marbles:
- 5 red
- 4 black
- 3 yellow
- 2 green
- 1 blue
You close your eyes and select a marble at random. You then place that marble back in the jar and add one more marble of the same color. For example, let’s say you reach in and grab a yellow marble. You put the yellow marble back in the jar and add one more yellow marble so that there are now 4 yellow marbles in the jar. You repeat this game 100 times.
We can clearly see that starting out, some marbles have a higher chance of being selected than others. For example, there is a 33.3% chance (5/15) of selecting a red marble and only a 6.7% (1/15) chance of selecting a blue marble. The kicker is that, because of the difference in starting points as you select red marbles you end up also adding more red marbles, increasing the probability of selecting future red marbles even further! The red and black marbles begin with a higher number of connections than the other marbles and thus overtime their wealth in connections grows larger.
Let’s see what this looks like in an R simulation!
First, we create our initial starting values for the marbles in the jar:

Let’s play the game one time and see how it works. We reach in, grab a marble at random, and whatever color we get, we will add an additional marble of that same color back to the jar.
In this trial, we selected a green marble. Therefore, there are now 3 green marbles in the jar instead of 2.
If we were to do this 100 times, it would be pretty tedious. Instead, we will write a for() loop that can play out the game for us, each time selecting a marble at random and then adding an additional marble to the jar of the same color.
After running the loop of 100 trials, we end up observing the following number and proportion for each marble color:
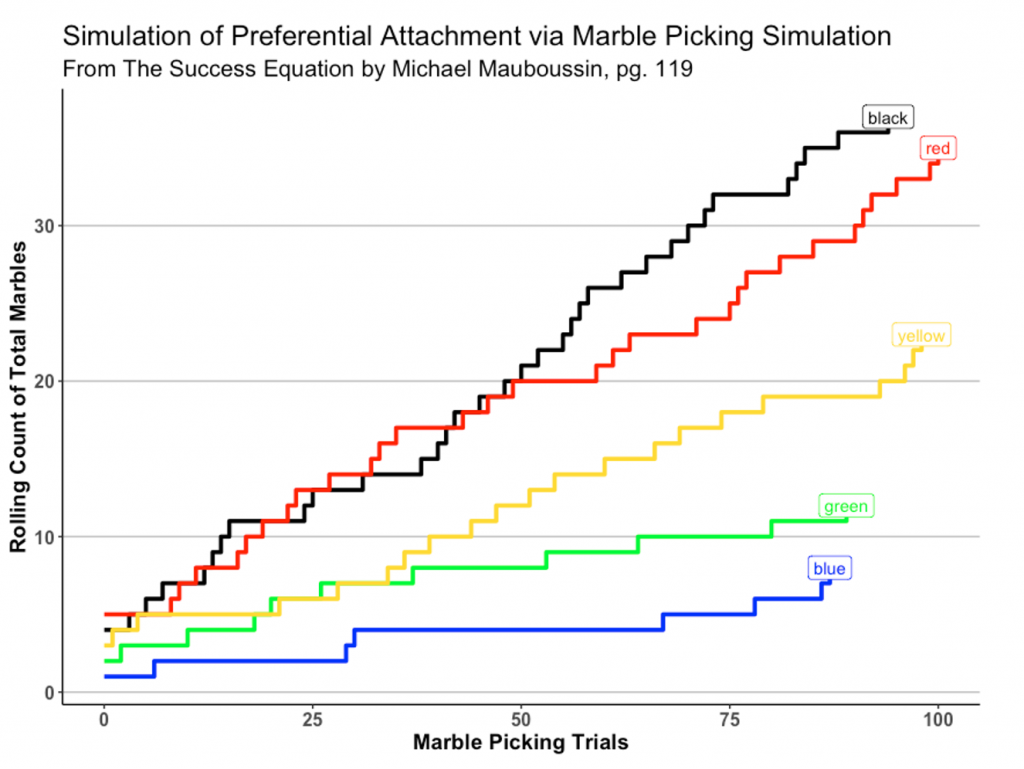
Notice that when we started 26.7% of the marbles were black and 6.7% were blue. After 100 trials of our game, black now makes up 32% of the population while blue is only at 7%. Remember, these are random samples, so it is pure chance as to which marble we select in each trial of the game. However, the initial conditions were more favorable for black and less favorable for blue, creating different ending points.
We can take our simulated data and build a plot of the trials, recreating the plot that Mauboussin shows on page 121:
The visual is not exactly what you see on pg. 121 because this is a random simulation. But we can see how each marble grows overtime based on their starting point (which you will notice is different on the y-axis at trial number 0 – the initial number of marbles in the jar).
If you run this code yourself, you will get a slightly different outcome as well. Try it a few times and see how random luck changes the final position of each marble. Increase the number of trials from 100 to 1,000 or 10,000 and see what happens! Simulations like this provide an interesting opportunity to understand the world around us.
The code for creating the simulation and visual are available on my GITHUB page.